|
|
|
|
|
|
|
category but a complex unit 'woven' from the simple feet.63 Socrates goes on to say that Damon evaluated the various rhythms and the tempi associated with them, condemning some and praising others. |
|
|
|
|
|
|
|
|
Plato hints at a parallelism between the series of rhythmic ratios and those governing harmony.64 Pythagoreans would certainly have seen a deep significance in this.65 The parallelism went further for those who recognized 4:3 as a valid rhythmical genus.66 Most writers, however, acknowledge only the three categories, equal (1:1), double (2:1), and hemiolic (3:2). This is the position of Plato, Aristotle, Aristoxenus, and others.67 |
|
|
|
|
|
|
|
|
Aristoxenus' work on rhythm is known to us from a nine-page fragment of the second book of his Elements of Rhythm, a short excerpt from another work of his On the Time-unit, a papyrus fragment from a treatise either by Aristoxenus himself or by some follower, and echoes of his doctrines in later sources, especially Aristides Quintilianus and Michael Psellus' Preliminaries to the Science of Rhythm.68 He took pains to define rhythm and to delimit musical from other forms of rhythm. As a good Aristotelian he distinguished the object shaped by rhythmlanguage, melody, or bodily movementfrom the rhythmic form shaping it. Thus he rejected the notion of earlier rhythmicians who thought that rhythm could be measured by syllables.69 Rhythm was an organization of |
|
|
|
 |
|
 |
|
|
63 'Compound' means resolvable into smaller constituents, cf. Aristox. Rhythm. 2.26, Aristid. Quint. p. 33.16. Enoplian and dactyl also appear as key terms of rhythmic theory in Ar. Nub. 651. One scholiast on that line identifies enoplian with the cretic 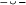 , a rhythm certainly sometimes associated with the dances in armour from which 'enoplian' took its name. But usually enoplian as a metrical term stands for , a rhythm certainly sometimes associated with the dances in armour from which 'enoplian' took its name. But usually enoplian as a metrical term stands for 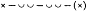 or something similar. See my Greek Metre, 195. or something similar. See my Greek Metre, 195. |
|
|
|
 |
|
 |
|
|
64Resp. 400a, 'there are three forms [i.e. ratios] from which step-sequences are woven, just as among notes there are four (forms) from which all harmoniai come'. He probably means the ratios 2:1, 3:2, 4:3, and 9:8. Cf. Barker, GMW i. 133 n. 35. |
|
|
|
 |
|
 |
|
|
65 Cf. Dionysius Musicus ap. Porph. in Ptol. Harm. p. 37.17, Aristid. Quint. p. 66. 1, Psell. Rhythm. 11. |
|
|
|
 |
|
 |
|
|
66 'Some' ap. Aristid. Quint. pp. 33.30, 38.20; Dionysius loc. cit.; Psell. Rhythm. 9. |
|
|
|
 |
|
 |
|
|
67 Pl. loc. cit., Arist. Rh. 1409d2-4, Aristox. Rhythm. 2.30ff., Aristid. Quint. p. 33.29; other references above, p. 131 n. 7. |
|
|
|
 |
|
 |
|
|
68 The relevant section of Aristides Quintilianus is 1.13-19 pp. 31.3-40.25; cf. Barker, GMW ii. 433-45. The other texts are collected with translations and notes by L. Pearson, Aristoxenus, Elementa Rhythmica (Oxford, 1990). The papyrus is POxy. 2687. |
|
|
|
 |
|
 |
|
|
69 The criticism, recorded by Psellus 1, may have been directed against Phaedrus, an otherwise unknown writer whose definition of rhythm as 'the measured placing of syllables in a certain mutual relationship' is listed before Aristoxenus' by Bacchius p. 313.2. |
|
|
|
|
|