|
|
|
|
|
|
|
freedom enshrined in the laws of melody, namely that tetrachords could be conjunct or disjunct. For example, suppose you were in chromatic Phrygian and you went up from Hypate to Mese, e f 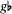 , a. You might continue up to Paramese, b, the start of the disjunct tetra-chord, but then proceed as if that note were the meeting-point of two conjunct tetrachords, and descend b , a. You might continue up to Paramese, b, the start of the disjunct tetra-chord, but then proceed as if that note were the meeting-point of two conjunct tetrachords, and descend b 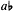 , g , g 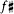 . Aristoxenus would say that you had turned Paramese into Nete (diezeugmenon), and modulated to a key in which that degree stood at the same pitch as Phrygian Paramese; a key, in other words, a fourth lower than Phrygian. All such conjunct-disjunct modulations, interpreted on the same principle, implied keys a tone, a fourth, or a fifth removed from the original one, reflecting the intervals involved in the collocation of tetrachords. . Aristoxenus would say that you had turned Paramese into Nete (diezeugmenon), and modulated to a key in which that degree stood at the same pitch as Phrygian Paramese; a key, in other words, a fourth lower than Phrygian. All such conjunct-disjunct modulations, interpreted on the same principle, implied keys a tone, a fourth, or a fifth removed from the original one, reflecting the intervals involved in the collocation of tetrachords. |
|
|
|
|
|
|
|
|
These, said Aristoxenus, were the harmonious types of modulation; but there were many other sorts, more or less harmonious according to how much the keys concerned had in common. They could be anything from a semitone to a whole octave apart.29 We do not know the details of his workings.30 But he found it necessary to have keys at regular semitone intervals over a whole octave. |
|
|
|
|
|
|
|
|
In naming them he adapted existing nomenclature. He used the seven names which Eratocles had applied to his enharmonic octave species, and which others had perhaps translated into diatonic terms: Mixolydian for the B species, Lydian for the C, Phrygian for the D, Dorian for the E, Hypolydian for the F, Hypophrygian for the G, and Hypodorian for the A. In the table of keys, to cancel out the pitch differentials, the sequence of names and intervals had to be inverted, with Hypodorian the lowest and Mixolydian the highest. The series of intervals separating these seven keys was thus the inversion of that in the note-series B C D E F G A; it was T T S T T S, which we can most simply represent by the note-series G A B C D E F, though it must be stressed that these notes have no significance for the keys in themselves but serve simply as a code indicating their relative positions: |
|
|
|
 |
|
 |
|
|
29 Cleon. pp. 205. 6-206. 2; cf. Arisrid. Quint. p. 22. 15ff. |
|
|
|
 |
|
 |
|
|
30 For a recent attempt to reconstruct them see Barker, GMW ii. 23-5. |
|
|
|
|
|