|
|
|
|
|
|
|
The lyra tunings are classified simply as 'hard' and 'soft', 'hard' being pure tonic diatonic and 'soft' being its conjunction with tense chromatic. |
|
|
|
|
|
|
|
|
We observe in the kithara tunings that the notes e-a-b-e' remain constant, giving a framework of fourths and fifths; and in each scale either the a or the b has notes making a fourth both above and below it, in other words either 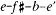 or e-a-d'-e'. No more than four out of eight strings had to be adjusted in substituting one of these scales for another. or e-a-d'-e'. No more than four out of eight strings had to be adjusted in substituting one of these scales for another. |
|
|
|
|
|
|
|
|
From one point of view, e-a and b-e' can be regarded as disjunct tetrachords with movable inner notes. However, they do not necessarily correspond to the tetrachords of Greek theoretical analysis. The latter exist on an abstract scale which can be variously calibrated against the scale of an actual piece of music. In the above scales the tetrachords of theory, which have the smallest interval at the bottom, may begin on the first and fifth degrees (Parhypatai, Lydia), on the second and fifth (Tritai, Tropoi), on the second and sixth (Hypertropa), or on the third and sixth (Iastiaiolia), and they may run off the end of the scale. I explain this here only so that the reader may be able to work out how it is that Ptolemy's analysis into soft diatonic, tonic diatonic, etc., fits the actual note-series. Fuller explanation of this aspect of Greek theory must await Chapter 8. |
|
|
|
|
|
|
|
|
So far we have been investigating scale structures without considering their extension. In dealing with Western music the question hardly arises. It is taken for granted that a scale once defined for an octave repeats itself indefinitely in higher or lower octaveswhich we see plentifully laid out on our piano keyboardand that the music may roam freely up and down as far as the compass of voices or instruments may allow. Our names for notes repeat at the octave, and we tend to think of a high C and a low C as being essentially the same note, much as the dustmen come on the same day one week after another. We call it the same because it stands in the same position in a structured series. |
|
|
|
|
|
|
|
|
We should beware of projecting this way of thinking upon the ancient or ethnic musician. Primitive melody, on the whole, does not extend much, if at all, beyond the range of a single octave, and it often restricts itself to a narrower compass than that. It may use just five or |
|
|
|
|
|