|
|
|
|
|
|
|
very strong reason to divide our octave into fourth + fifth (C-F-C) or fifth + fourth (C-G-C), or both at once (C-F-G-C). This is the most natural and fundamental principle of division of the octave, and any other principle that is applied must be subordinated to it. Now, if we make a division into twelve semitone steps, a fourth will correspond to five steps and a fifth to seven. But if the keyboard were laid out as above, with an unvarying alternation of white and black notes, then either a fourth or a fifth taken from a white note would land us on a black note, whereas the purpose of distinguishing white and black is to line up the notes of our basic melodic scale on the whites. The asymmetric grouping achieves this aim. |
|
|
|
|
|
|
|
|
To reach the fourth we take two melodic steps of a tone and one of a semitone (not necessarily in that order); for a fifth, it is three tones and a semitone. But why have we made our characteristic melodic step the tone, a unit that does not fit a whole number of times into either fourth or fifth? Where does this unit come from? |
|
|
|
|
|
|
|
|
The answer is that it appears in the first instance as the difference between the fourth and the fifth. If you construct a fourth and a fifth up from C (or what comes to the same thing, a fifth up from the lower C and another down from the upper one), you get two notes (F and G) between which this new interval of a tone is automatically born. It corresponds to the ratio 9:8 (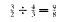 ). And it easily reproduces itself. If you have the skeleton structure C-F-G-C, and you take a fourth down from G and a fifth back up, you make C-D-F-G-A-C. Repeat the operation from A, and you have C-D-E-F-G-A-B-C: all of the white notes. Repeat it again from B, and you start filling in the black notes. Soon your keyboard is complete. Further cycles of fourths and fifths will only make the same notes recur. |
|
|
|
|
|
|
|
|
However, by their third appearance, if your fourth and fifths have been perfectly true ones, and you have a reasonable ear, it will be starting to become apparent that something is amiss. Your notes are now about a quarter of a tone out of tune. The longer you go on re-inventing them, the worse it gets. The reason is that the apparently coherent system has a hidden flaw, a design fault. When you take two 9: 8 tonal bites out of a fourth (C-F, or G-C), what is left (E-F, B-C) is not a true semitone but something slightly smaller, actually 12 per cent smaller. The inaccuracy perpetuates and compounds itself. None of the black notes constructed as above will divide the tones into equal halves. The second time round the inequality will be greater. |
|
|
|
|
|